Does a Higher Advertised Return Make a Better Investment?
Spoiler alert: I’m going to give you the moral of this story right up front.
Do not choose one investment over another simply because it advertises a higher rate of return.
I’ve been guilty of precisely this mistake on many occasions, and suffice it to say, it’s gotten me into trouble.
This was especially true early on in my investing career. I would look at two passive real estate investments: one with an Internal Rate of Return (IRR) of 12%, and another with an IRR of 24%.
“Well,” I thought, “if the 24% return deal performs even half as well as they predict, then worst case, it’ll still match the 12% deal.”
Just like that, my decision was made.
However, I’ve learned that this method is completely wrong, and for two big reasons:
- Risk
- Assumptions and Manipulation
But before we get into those, let’s quickly review a couple of definitions (for a full analysis of these concepts, be sure to check out this article).
Two Main Types of Return Metrics
There are two main types of returns you’ll usually see advertised in real estate deals: Internal Rate of Return (IRR) and Equity Multiple (EM).
IRR is a return-on-investment calculation that also takes into account the “time value” of money. The idea is that money will be worth less in the future–partially due to inflation, but also because the money tied up in an investment could have been used to invest elsewhere in the meantime. The IRR seeks to take all of this into account.
Equity multiple is another ROI calculation that takes more variables into account. This ‘equity multiple’ of an investment is the cumulative distributed returns divided by the paid-in capital.
In other words, it’s the total amount returned to you over the life of the investment divided by the amount you initially invested.
Ideally, in assessing a potential investment, you would use both of these metrics. This will give you a better idea of what to expect.
With that out of the way, let’s take a look at why basing your investment decisions solely on the predicted rate of return can lead to trouble.
Risk
Why is it that your online savings account offers you an interest of 1%, while certain other investments offer up to a 900% return? Who wouldn’t want to get nearly 10x their original investment back?
The reason is simple, and it’s a little something called risk. Risk can be summed up with this simple question: what are the chances that the expected return will become reality?
Well, when it comes to interest received from a bank, it’s as close to complete certainty as you can get. On the flip side, little risk means little reward.
However, when it comes to certain other investments, like angel investing, the potential for success is far lower. The rate of return reflects that, with some investments bringing back ten times your initial investment.
To account for this, you might hear of something called “risk-adjusted returns.” This is another metric you should utilize.
You’ll find the best example of risk-adjust returns in a casino. Here, returns are based on odds. Yes, they’re tipped in the casino’s favor, but the returns are proportional to the odds–or “risk.”
The thing is, in real life, it’s not so linear.
Since the real estate market isn’t totally efficient and therefore unpredictable, you might find a real estate investment with a lower return and higher risk, or a higher return and a lower risk, all within the same market.
The key is to identify where the scale is tipping. This, in turn, can only be assessed by performing thorough due diligence.
The bottom line is this: the higher the advertised rate of return, the more risk is likely associated with the deal. Well, that’s what you should probably initially assume and look for ways why the deal makes sense.
Assumptions and Manipulation
Whenever you see a pro forma or deck (the investment proposal), you’ll be presented with several metrics. But if you’re like me in my early days of investing, you’re likely to focus solely on the return.
Two of the metrics you’ll see are the aforementioned equity multiple and the internal rate of return.
These will tell you what to expect in terms of returns for investing your capital, and they do a much better job of giving you the big picture (when used together).
Equity multiples are easier to understand, so let’s start there. With this metric, returns are usually defined in terms of what you started with and how much you got back. For example, should you expect to get 1.5x your money or 2x your money back?
The thing is, you have to consider how long the project will be. 2x your investment in four or five years sounds pretty great, but 2x over ten years isn’t nearly as good.
This is why equity multiple alone isn’t quite good enough to give you the whole picture.
This is where IRR comes in. As mentioned, IRR takes into account the time value of money. All cash flow matters, and the timing of those payouts is equally important.
IRR is probably the best metric used to compare different investments. However, again, many people simply invest based on the highest one.
The problem is, by simply changing some assumptions, IRR can easily be manipulated.
If you change the assumption of a refinance and return of capital, or if you simply change the timing of returns, it can change the IRR.
Here’s an example where I show how two investments can actually get the same overall return in dollars, and the same EquityMultiple, but depending on how distributions are given out, it can dramatically change the IRR.
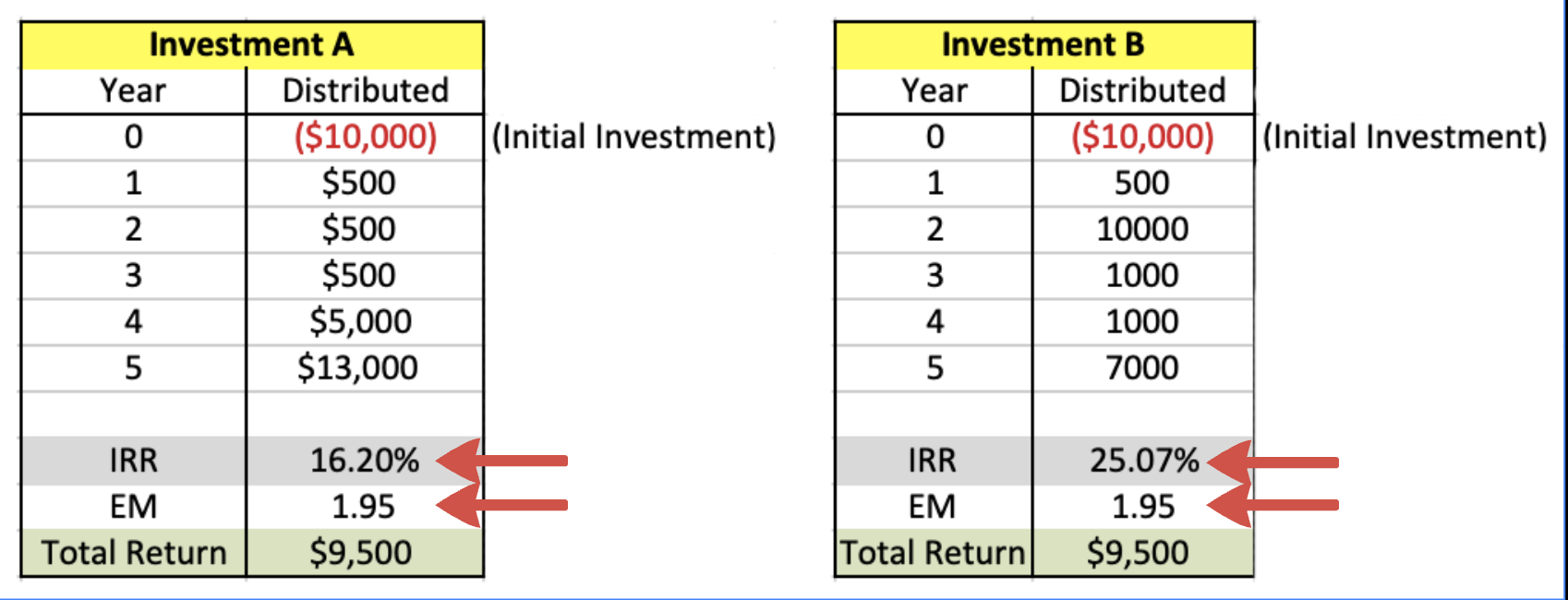
Again, the IRR is simply calculated using a calculator and formula that takes into account the time value of money. The sooner you get your money back, as well as returns, the higher the IRR.
There is another aspect of the IRR to consider as well, and that is exactly what it takes into account.
Gross IRR, for example, does not account for fees.
Net IRR does take fees into account, and this is typically the number to focus on.
However, even when you are given this metric, it’s not always easy to tell if it’s referring to the net or the gross IRR.
It is important, though, to know exactly which one you’re being presented with, as the difference can vary by several percentage points. You may have to contact the manager of the deal in order to get this information.
The bottom line here is that you will likely be presented with different metrics for the potential return an investment will give you, and some of those metrics can be easily manipulated to appear better than they really are.
My Experience & Wrapping It Up
Without bringing up too many painful details from the past, I’ve invested in “safe” deals that promised 12% returns where I’ve received closer to 18-20% returns, and I’ve invested in deals where I expected 22% returns and literally lost money on them. So to spell that out, I’ve received a negative return before.
At the end of the day, advertised returns are just one part of the equation. You have to trust that the sponsors actually have the ability to deliver on those numbers, and then you need to check the assumptions.
When choosing an investment, you really can’t rely on an advertised number at all. There are a ton of different variables, and each one should be carefully weighed. Ultimately, everything must work together in a way that fits your personal investment goals.
Personally, I like to invest with multiple different sponsors to see how they operate and in the end, see how well true returns match up with predicted returns.
Then I can make a truly informed decision about what I think the best investment will be.
PIMD





0 Comments